5 Ways Median Beats Average
When discussing statistical measures, two terms often come up: median and average (or mean). Both are used to describe the central tendency of a dataset, but they serve this purpose in different ways and are suited to different types of data. Understanding the distinction between median and average is crucial for making informed decisions in various fields, from economics and finance to social sciences and healthcare. In certain contexts, the median offers a more reliable or meaningful insight into the data than the average. Here are five ways the median beats the average in data analysis.
1. Resistance to Outliers
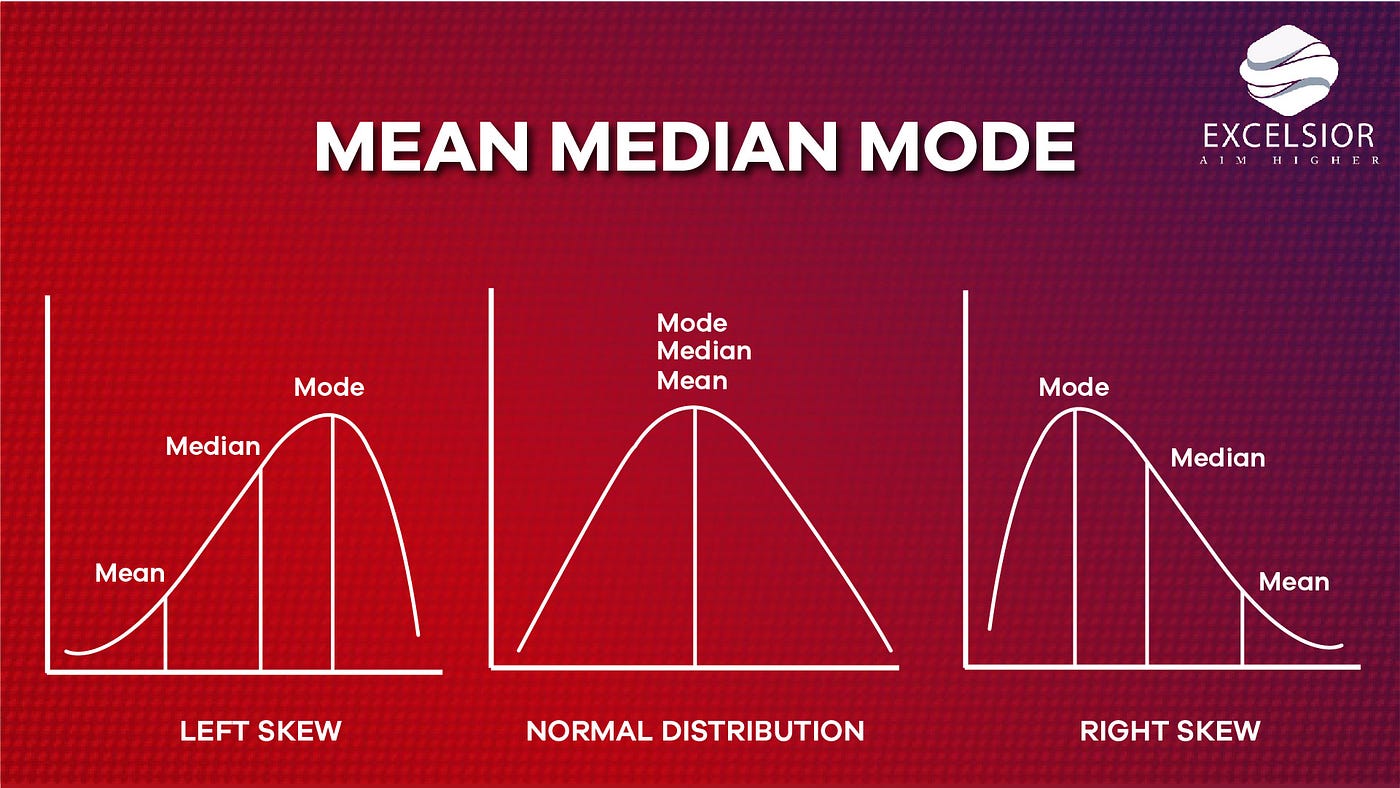
One of the primary advantages of the median over the average is its resistance to outliers. Outliers are data points that are significantly higher or lower than the other observations in the dataset. The average is highly sensitive to outliers because it includes every value in the calculation. A single very high or very low value can skew the average, making it less representative of the typical value in the dataset. On the other hand, the median is more robust against outliers. When data is arranged in ascending or descending order, the median is the middle value (or the average of the two middle values if there is an even number of observations). Outliers at the extremes of the data distribution do not affect the median as much as they affect the average, making the median a better choice for describing datasets with outliers.
2. Skewed Distributions
In many real-world scenarios, data follows a skewed distribution rather than a symmetrical, normal distribution. Skewness occurs when the data distribution is asymmetric, meaning it has a longer tail on one side than the other. In such cases, the average can be pulled in the direction of the skew, leading to a value that is not typical of most data points. The median, being the middle value, is less affected by skewness and provides a better representation of the central tendency in skewed distributions. For instance, in income distributions, which are often highly skewed due to very high incomes among a small percentage of the population, the median income is usually a more accurate representation of the “typical” income than the average income.
3. Interpretability in Non-Numeric Contexts
While averages are excellent for numerical data, medians can be more interpretable in certain non-numerical or semi-numerical contexts. For example, when dealing with ranked data or categories that have a natural order but are not necessarily numerical (such as satisfaction ratings on a scale from 1 to 5), the median can provide a more intuitive understanding of the central tendency than the average. This is because the median directly reflects the middle ranking or category without requiring the assignment of numerical values that might not accurately capture the nuances of the rankings.
4. Easier to Understand for Non-Technical Audiences
For non-technical audiences, the concept of the median can be more accessible than that of the average. The idea of a “middle value” is straightforward and easy to grasp, even for those without a strong statistical background. In contrast, calculating an average involves adding all the values and then dividing by the number of values, a process that, while simple, can seem abstract or complex to those unfamiliar with statistical concepts. Therefore, when communicating insights to a broad audience, using the median can facilitate a clearer understanding of the data’s central tendency.
5. Decision Making in Risk-Averse Contexts
In risk-averse contexts or when the cost of exceeding a certain threshold is very high, the median can be a more appropriate measure for decision-making than the average. This is because the median focuses on the middle value, providing a clearer picture of what a “typical” outcome might be, without being unduly influenced by extreme values. For instance, in financial planning or insurance underwriting, understanding the median outcome or exposure can be crucial for managing risk, as it gives a better indication of the most likely scenarios than the average, which could be skewed by rare but high-impact events.
In conclusion, while both the median and the average are valuable statistical measures, the median has several advantages that make it preferable in certain situations. Its resistance to outliers, applicability to skewed distributions, interpretability in non-numerical contexts, ease of understanding, and utility in risk-averse decision-making contexts all contribute to its versatility and usefulness in data analysis. By choosing the right statistical measure for the context, analysts and decision-makers can gain more accurate insights into their data and make more informed choices.
What is the main difference between the median and the average?
+The main difference between the median and the average is how they are calculated and how they represent the central tendency of a dataset. The average (mean) is calculated by adding up all the values and dividing by the number of values, whereas the median is the middle value in a dataset when it is ordered from smallest to largest. The median is less affected by extreme values (outliers) and is more suitable for skewed distributions.
When should the median be used instead of the average?
+The median should be used instead of the average in several situations: when the data contains outliers, as the median is more resistant to their effect; when the data distribution is skewed, as the median provides a better representation of the central tendency; and in contexts where the concept of a "middle" value is more intuitive or relevant for the analysis or decision-making process.
Can the median and average ever be the same value?
+Yes, the median and average can be the same value. This typically occurs when the dataset is symmetrically distributed, such as in a normal distribution, where the mean, median, and mode are all equal. In such cases, both the median and the average provide an accurate representation of the central tendency of the data.
Choosing between the median and the average depends on the nature of the data and the context of the analysis. Understanding the strengths of each measure can significantly enhance the accuracy and relevance of statistical insights, leading to better-informed decisions across various fields.
By acknowledging the unique benefits of the median in data analysis, analysts can enhance their toolkit for understanding complex datasets and communicating findings effectively to both technical and non-technical audiences. The median’s robustness and interpretability make it an indispensable statistical measure for gaining deeper insights into the central tendency of datasets, especially in scenarios where the average might not fully capture the essence of the data.



